Fuzzy matching: 4 methoden om een koppeling te makken

In een vorig artikel liet ik u kennismaken met een oplossing voor een fuzzy matching tussen 2 verschillende tabellen. Daarin vergeleek ik 2 ETL-oplossingen (Extract Transform Load). Tableau Prep Builder gaf niet het gewenste resultaat en daarom wendde ik me tot Anatella. In het artikel van vandaag onderzoek ik de verschillende algoritmes van Fuzzy Matching die beschikbaar zijn in deze tool evenals de resultaten ervan. Zoals u zult merken, komt één algoritme eruit als winnaar.

Inleiding

Wanneer u een koppeling wilt maken tussen meerdere tabellen zijn er 2 mogelijkheden. Ofwel volgt uw verbindingssleutel exact dezelfde benamingen in beide tabellen, ofwel niet. Als u in het gezegende geval van de 1e situatie bent, ga dan gerust door met wat u bezig was. Dit artikel zal u dan niets bijbrengen. Als u daarentegen in het tweede geval zit (of gewoon nieuwsgierig bent), wens ik u veel leesplezier.

Fuzzy matching algoritmes

In de casestudy die ik voorstel, wordt fuzzy matching uitgevoerd op een verbindingssleutel met landnamen erin.
Er bestaan heel wat methoden om de gelijkenis tussen 2 entiteiten te berekenen. Wat ik mooi vind aan Anatella is dat het je, in tegenstelling tot andere ETL’s, de keuze biedt tussen 4 methoden:

• Damereau Levenshtein-afstand
• Damereau Levenshtein-gelijkenis (hetzelfde als de afstand, zelfs tussen 0 en 1)
• Jaro-Winkler-gelijkenis
• Dice-gelijkenis

Er bestaan natuurlijk andere methoden om de overeenkomst te berekenen. Raffael Vogler (Engelse site) geeft een goed overzicht van de verschillende technieken die beschikbaar zijn in het “stringdist”-pakket voor R.

Jaro-Winkler-gelijkenis

Deze methode dateert uit 1999 en vloeit voort uit de methode van Jaro (1989). De verkregen score varieert tussen 0 en 1 en wordt berekend door de overeenkomstige karakters in de ene string en vervolgens in de andere string te vergelijken, rekening houdend met de karaktertransposities.

Damereau Levenshtein-afstand

Dit is een oude methode (1964) die het mogelijk maakt om het aantal stappen te berekenen dat nodig is om een string a om te zetten in een string b. De toegestane bewerkingen zijn verwijderen, invoegen, vervangen van een enkel karakter, transpositie van 2 aangrenzende karakters. De berekende afstand is dus een geheel getal dat overeenkomt met het aantal stappen dat nodig is voor de transformatie (0 als strings a en b identiek zijn).

DICE-gelijkenis

Ook dit is een oude methode (1948). Ze bestaat uit een eenvoudige vergelijking van de cijfers. De coëfficiënt ligt dicht bij de Jaccard-index. Ik verwijs u naar de Wikipedia voor enkele veelzeggende voorbeelden.

De resultaten

Hieronder de resultaten. Ik herinner u eraan dat deze resultaten niet in elke situatie kunnen worden omgezet. Elk geval moet vooraf worden onderzocht om de meest geschikte methode te vinden. In dit geval hebben we het over fuzzy matching tussen landnamen die overeenkomen met verschillende benamingen. Ik verwijs u naar mijn artikel van vorige week voor de lijst.

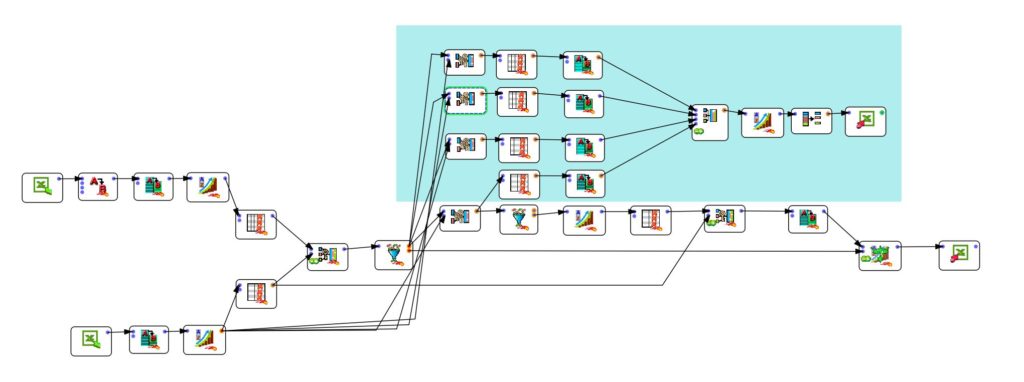
Om de resultaten van de verschillende algoritmen te kunnen vergelijken heb ik gewoon de stroom in de ETL (Anatella) lichtjes aangepast om de 4 voorgestelde “fuzzy joints” te kunnen vergelijken. Het proces is op onderstaand diagram in blauw weergegeven (klik erop om het te vergroten).

Om het lezen te vergemakkelijken, heb ik de resultaten geëxporteerd naar een Excel-bestand (hier te downloaden).

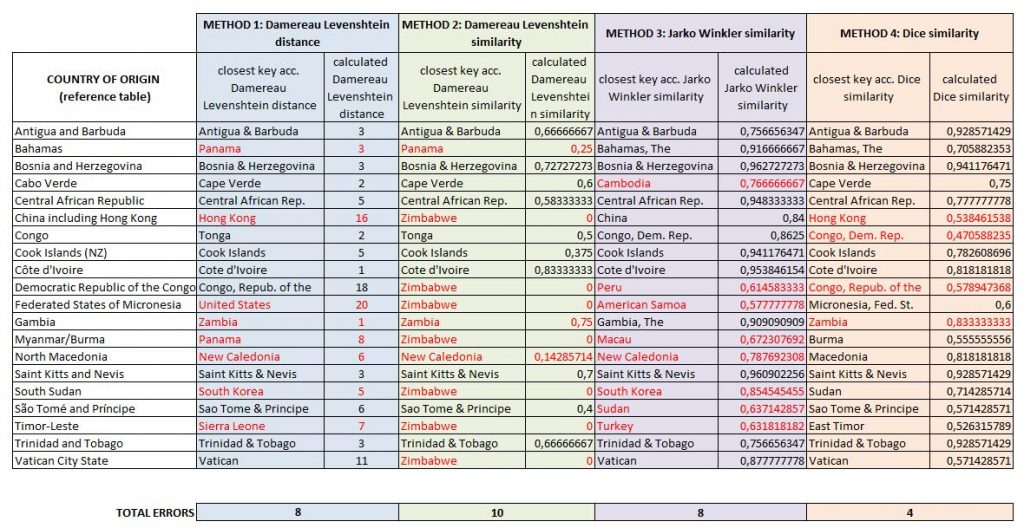
De resultaten zijn soms verrassend.

Methode 2 lijkt de voorkeur te hebben voor Zimbabwe en verschilt van methode 1 (a priori dichtbij). De fouten in classificatie zijn soms groot (South Sudan / South Korea).

Methode 3 (Jaro Winkler) werkt iets beter, maar nog altijd met te veel foute classificaties. Het heeft wel een groot voordeel (zie volgende paragraaf).

Methode 4 (Dice-overeenkomst) geeft de beste resultaten. De slechte classificatie van Hongkong (zie vermelding in de referentietabel) kan te wijten zijn aan voor de hand liggende redenen. De fout met “Gambia” is gemakkelijk te verklaren door de digrammatische benadering van de Dice-Sorensen methode.

Definitie van een drempelcoëfficiënt

Om te voorkomen dat er fout-positieve of fout-negatieve resultaten ontstaan, is het nuttig om een drempelwaardecoëfficiënt te bepalen voor het verwerpen van resultaten die handmatig moeten worden verwerkt.

Voor de methode van Damereau-Levenshtein (methode 1 en 2) zien we dat deze aanpak niet erg efficiënt is, omdat het algoritme valse positieven geeft met lage berekende afstanden (zie Bahamas, Gambia, North Macedonia, South Sudan).

Voor Dice zou het definiëren van een drempel rond 0,5 de 2 vals-positieven niet hebben gedetecteerd en zou het ook een vals negatief hebben opgeleverd (Congo).

Voor methode 3 zou het instellen van de drempel op 0,8 alle gemiste overeenkomsten hebben geëlimineerd, maar zou eveneens een fout-negatief hebben opgeleverd (Trinidad en Tobago).

Conclusie

De methode van Dice (ook wel de methode van Sorensen genoemd) levert in deze oefening de beste resultaten op om een fuzzy matching tussen landnamen te realiseren. De Jaro-Winkler methode maakt het mogelijk om een drempelwaarde van 0,8 te definiëren, waardoor de niet overeenkomende resultaten nauwkeurig worden verwijderd.

Source: IntoTheMind