This option is only available when the “Save Core” option is disabled.
This will generate a prediction file that contains:
Let’s now illustrate how the distance to the nearest segment is computed. We will first give an easy example: Let’s assume that we have three segments Red, Green and Blue. A new individual ‘A’ arrives:
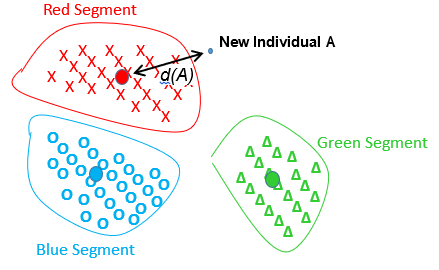
Everything is fine: The individual ‘A’ belongs to the Red Segment because it’s the closest one. The distance from the individual ‘A’ to the Red Segment is noted ‘d(A)’.
If the segments are non-spherical, we were forced to use the “Minimum Spanning Tree” (MST) algorithm. When we are using the MST algorithm, the distance to the nearest segment is computed in a special way. Let’s go back to the second example of section 5.5.3.2:
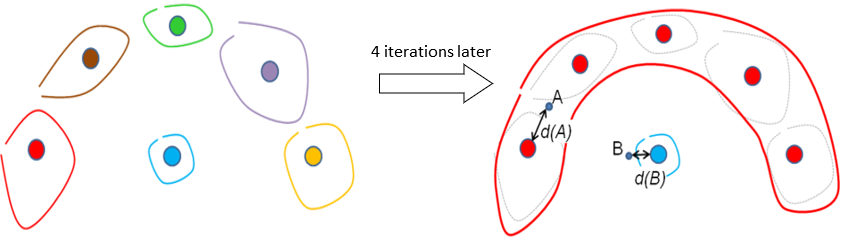
The main question is: “Which point (A or B) has the smallest distance to its own segment?” (The point ‘A’ belongs to the Red Segment and the point ‘B’ belongs to the Blue Segment). This question is interesting when you want to select the “real core” of each segment.
The distance from the individual ‘A’ to the Red Segment is noted ‘d(A)’.
The distance from the individual ‘B’ to the Blue Segment is noted ‘d(B)’.
Based on the distances ‘d(A)’ and ‘d(B)’, we can say that ‘B’ is the answer to the above question (because ‘d(B)<d(A)’ ). But graphically, we see the opposite! The point ‘A’ is the closest to its own (red) segment: it’s in the middle of it! … and B is really far apart from the blue segment! Obviously, there is something wrong here.
To correct this (bad) situation, you can ask StarDust to add some “intermediate centers”. For example, when you enter: 
... you will have 2 additional “intermediate centers” (illustrated below with small crosses) that will be used to compute the distance to the nearest segment:
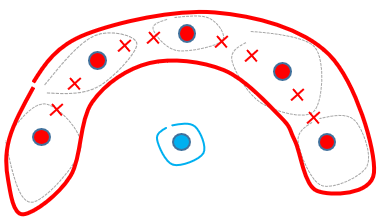
Using these “intermediate centers”, we now have ‘d(A)<d(B)’ which is correct: The issue is solved!