Let’s now take a more real example. Let’s assume that we have a dataset with 2 columns that are the 2 dimensions used inside the Euclidean Distance used to construct the segments. These 2 columns are:
1.Age expressed in Year 0 < Age < 100
2.Size expressed in Meter 0 < Size < 2
The classical Euclidian Distance is:
This distance, however, is not very good.
Let’s take an example. Let’s compute the distance between 3 individuals: A, B and C.
A and B are separated by one meter of size. So the distance between A and B is one.
In opposition, B and C are separated by 10 years. So the distance between B and C is ten.
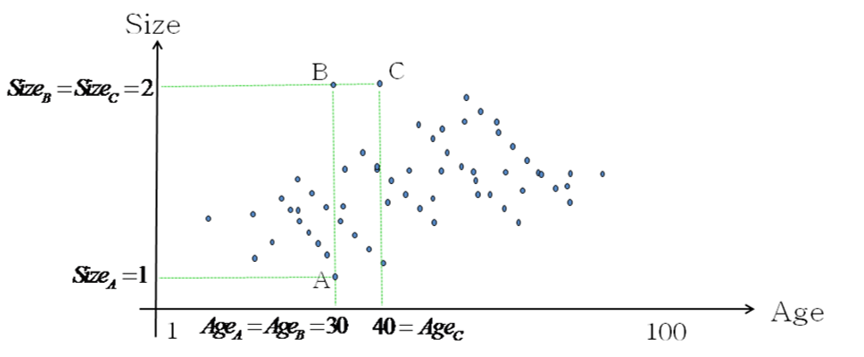
You can directly see that there is a problem here. Graphically, we can see that B is closer to C than A but the Euclidean Distance “says” the opposite:
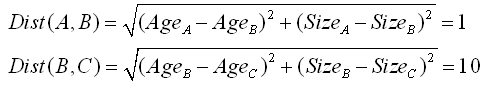
So, there is a problem in the Euclidean Distance. The problem comes from the fact that the “age axis” goes from one to one hundred… and the “size axis” only goes from one to two: The range of the two axises must be similar in order to have a meaningful distance.
To correct this unfortunate situation, we will define a “normalized-distance” where each axis has been normalized to obtain more or less the same range. For the “normalized-distance”, the “age” has been divided by one hundred and the size stays the same:
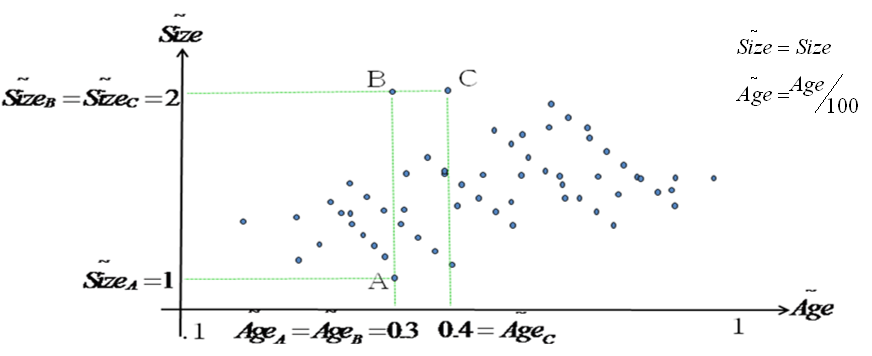
Using this new “normalized-distance”, now, we have:
It’s now ok: B is closer to C than A.
As a conclusion: Normalization is Important! We must always use « normalized - distance» !
If we compare the “standard-distance” with the “normalized-distance”, we can see that:
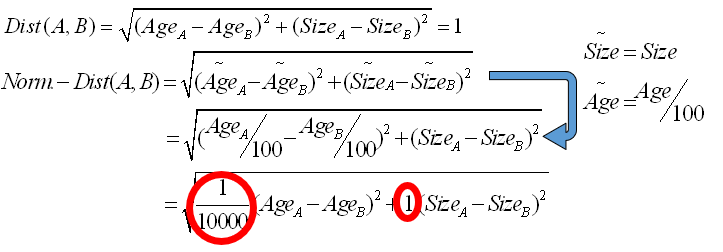
The equations defining these two distances are very close. There are nearly the same. The only difference is that, for “normalized-distance”, you have normalization factors (