<< Click to Display Table of Contents >> Navigation:  2. Introduction to the PCA techniques > 2.1. Dimensionality reduction > 2.2.2. A second example: from 3D to 2D

 

Here is another example:

 

 

 

 

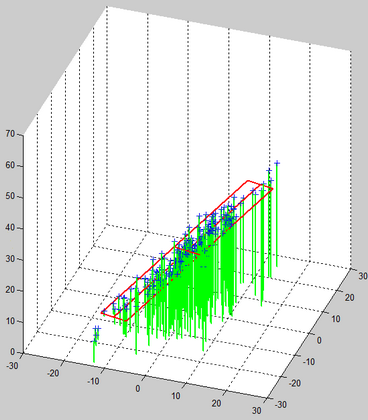
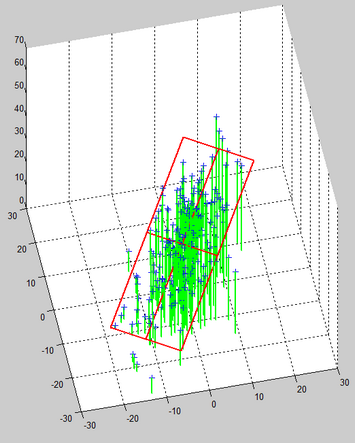
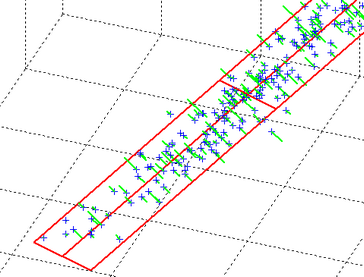
We start from 3D points and we want to reduce the dimension to 2D. The Points in 3D are in blue. The Projection of the points on the « floor » is represented with green lines. The PCA1 and PCA2 axises are in red.

 

Let’s project all the 3D points on the plane defined by the PCA1 and PCA2 axises. The points after projection are in Blue. The projection direction in itself is in green. Please, note that the distance between the points Before and After projection is very small, so we don’t lose much information when we are projecting all the points on the PCA plane (we didn’t disturb the “true original position” of the points too much when projecting):

 

 

 

 

 

 

 

 

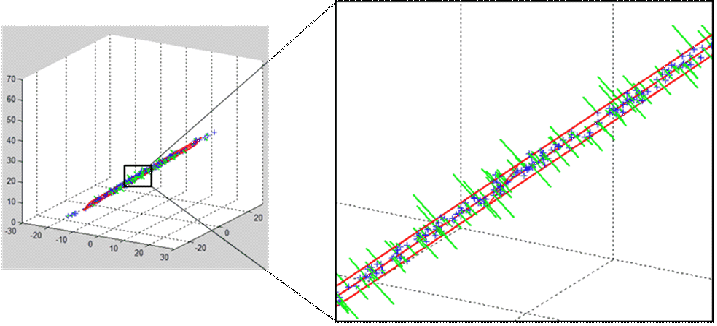
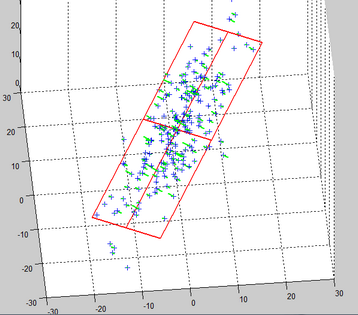
After projection, the 3D points are now in a 2D space formed by the PCA1 and PCA2 axises. We just reduced the dimension from 3D to 2D without losing too much information:

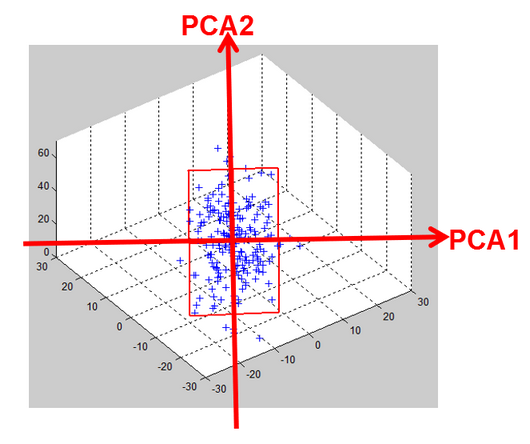
To summarize, the PCA is a technique that allows representation of high dimension « points » into a lower dimensional space. The first PCA axises are defining priviliged directions that are the best directions on which to « project » in order to « loose » as little information as possible.