There are 3 options for the “Similarity Measure”:
1.Damereau-Levenstein
2.Jora-Winkler
3.Dice Coefficient
The “Damereau-Levenstein” similarity measure is derived from the “Damereau-Levenstein” distance between two strings. This distance is defined in the following way:
The “Damereau-Levenstein” distance between 2 strings is the minimum number of operations needed to transform one string into the other, where an operation is defined as an insertion, deletion, or substitution of a single character, or a transposition of two adjacent characters.
We derive the “Damereau-Levenstein” similarity from the “Damereau-Levenstein” distance:
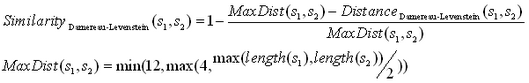
Here are some examples:
•The distance between “BRUSELS” (that we’ll define as the reference value) and “BRUSSSEL” is 3 because there are three errors:
othere are three “S” in the middle instead of one (2 insertions= 2 errors)
othe final “S” is missing.
•The distance between “BRUSELS” (once again, the reference value) and “BRUGELS” is 1 because there is only one error:
oThe “S” letter is replaced by the “G” letter
Let’s look at the above two examples: The “Damereau-Levenstein” distance finds that “BRUGELS” is closer to “BRUSELS” than “BRUSSSEL”?? There is something very wrong about that. The example illustrates that the “Damereau-Levenstein” distance…
1.…is worthless to compare strings when the distances between the strings might go above 1.
2.…is ignoring the phonetic content of the characters. If you are interested in a phonetic encoding, please refer to the section 5.9.2.
The Jaro-winkler similarity is an attempt to improve on the idea of the “Damereau-Levenstein” similarity. The Jaro-winkler similarity tries to stay meaningfull in the case where the “Damereau-Levenstein” distance fails: i.e. when the distance between the strings might go above 1. Extensive tests demonstrates that, in practically all real-world studies, the Jaro-winkler similarity outperforms the “Damereau-Levenstein” similarity. The exact definition of the Jaro-winkler similarity is well documented on internet and will not be reproduced here.
![]()
The documentation about the “Jaro-winkler similarity” is available on Wikipedia on a page named “Jaro-winkler distance”. This is somewhat disturbing because it’s actually really a similarity measure (the higher the value, the closer the two strings are) and not a distance measure.
Although the Jaro-winkler similarity is better than the “Damereau-Levenstein” similarity, it’s still limited to “small” strings (for example: city names, surnames, etc.) where the number of differences between the compared strings stays relative small because of the small sizes of the strings (After all, the “Damereau-Levenstein” is just an improvement on the “Damereau-Levenstein” similarity and finally suffers from the same defaults). Thus, if you want to compute similarities between very long strings (such as “street names”, long “product names”, long “SKU names”, long “Book titles”, etc.), you’d better use the “Dice Coefficient” (the “Dice Coefficient” is also sometime named the “Pair letters similarity”).
The “Dice Coefficient” is a similarity metric that rewards both common substrings and a common ordering of those substrings. The definition is:
![]()
The intention is that by considering adjacent characters (i.e. character-pairs), we take into account not only of the common characters, but also of the character ordering in the two strings, since each character pair contains a little information about the ordering. Here is an example:
![]()
Inside the Anatella implementation of the Dice Coefficient, all the letter-pairs that contains a space character are discarded before any computation. This means that the similarity between the strings "vitamin B" and "vitamin C" is 100%. In this case (when you are interested in correcting small differences), you should rather use the “Damereau-Levenstein” or “Jaro Winkler” similarity.