Let’s go back the “city name” example: i.e. We have a table with different city names, some of them have some spelling mistakes and we want to correct these mistakes.
We’ll typically have such a graph:
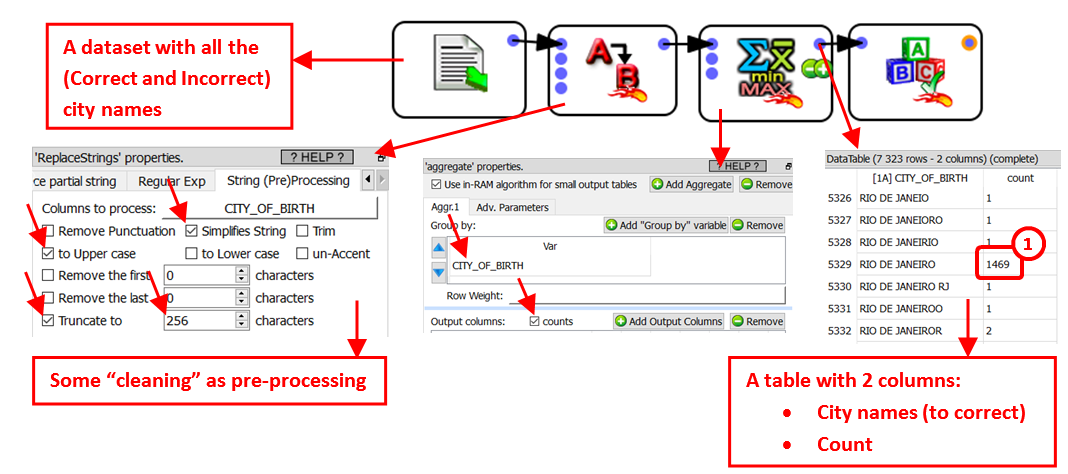
Some modalities (i.e. some strings) occurs very often (such as the string “RIO DE JANEIRO” that occurs 1469 times). ![]() These very “heavy” strings are assumed to contain the correct spelling of the city name.
These very “heavy” strings are assumed to contain the correct spelling of the city name.
Some other modalities practically never appears inside the text corpus (such as the string “RIO DE JANEIORO” that occurs only one time). These very “Light” strings (in opposition to the “heavy” strings) could easily be spelling errors. The threshold between a “Light” and a “Heavy” modality is given in parameter P3:

A given string is a spelling error (that must be corrected) if:
1.It’s a “Light” modality.
2.It’s “very similar” to (i.e. it “looks like”) another string X.
Depending on the parameter P4, the other string X can either be:
oA “heavy” string (This is, by far, the fastest option: Use this option if you have performance issue and the running-time is too long).
oAny string slightly heavier than the string currently being “corrected”.
The parameters P1 and P2 defines if two strings must be declared “very similar”.
What’s happening with the cities that have a small population in real-life? All these cities will only have a small representation inside the database (i.e. they will never be classified as “heavy” modalities). To still be able to correct the spelling mistakes of these “small cities”, you must set the parameter P4 to the value “regroup with any other modality” (this is actually the best choice, but it’s much slower).
All the strings that are spelling errors are “regrouped” with the string that is the most likely to have the correct spelling (i.e. with the most represented string). So, we can have the following re-groupings:
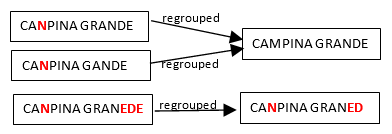
Hereabove, we see that many people make the same spelling mistake: i.e. They replace the “M” letter with the “N” letter inside the word “CAMPINA”. Let’s now assume that, after the corrections/regrouping illustrated above, we find the following two new “groups”:
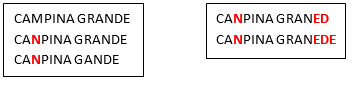
We see that, amongst the many people that erroneously write CANPINA (instead of the correct orthography “CAMPINA”), there are some people that don’t manage to write correctly the word “GRANDE” neither (i.e. they erroneously write “GRANED” or “GRANEDE” instead). The two groups illustrated above are quite similar because CAMPINA is written with exactly the same spelling mistake (“CANPINA”) in both groups. Thus, it would be nice if these 2 groups would new be merged together in a second iteration (because they most likely represent the same city “CAMPINA GRANDE”):
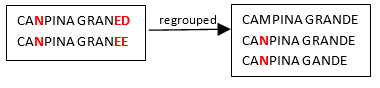
Such that we finally obtain one final group:

Note that these 5 strings could not be “regouped” together at the first iteration (for example, because “CANPINA GRANED” is “too far away” from “CAMPINA GRANDE”) …But the group containing “CANPINA GRANED” is similar enough to the group containing “CAMPINA GRANDE”, so that it’s still possible to regroup these 2 groups in a later iteration.
We can now give more details about the spelling-correction-algorithm used in Anatella:
The algorithm is:
1.Assign all initial strings into different groups (one string per group).
2.Consider all the “Light Groups” (i.e: the “Light Groups” are defined by “the sum of the occurrence of all the string’s weight inside a “Light Group” is below the threshold given in parameter P3”) in the order from the “lightest” to the “heaviest”: A given group can be merged with another group X if it’s “very similar” to this other group X.
The candidate groups X are selected based on the value of parameter P4.
Depending on the parameter P5, the similarity between two groups is …:
oP5 is not checked: … the average similarity between all the string-pairs.
This means that, in the above example, the similarity between our two groups is the average of the similarity between the following string-pairs:
( CANPINA GRANED , CAMPINA GRANDE )
( CANPINA GRANED , CANPINA GRANDE )
( CANPINA GRANED , CANPINA GANDE )
( CANPINA GRANEE , CAMPINA GRANDE )
( CANPINA GRANEE , CANPINA GRANDE )
( CANPINA GRANEE , CANPINA GANDE )
This is the best option, although it’s very slow.
oP5 is checked: … the similarity between the most represented string in each group.
This means that, in the above example, the similarity between our two groups is the similarity between the following 2 strings:
( CANPINA GRANED , CAMPINA GRANDE )
3.Decide if another iteration is required: If yes, go back to step 2.
The parameters P6 and P7 are used to decide how many iterations the algorithm does. Most of the time, one iteration is enough. Some time, two iterations can be useful (but the second iteration usually takes a huge amount of time).