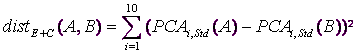A segmentation is based on a “distance-definition”.
Using StarDust, you can create very complex distance-definition. For example, the following axis can be included inside you distance-definition:
•On all continuous variables:
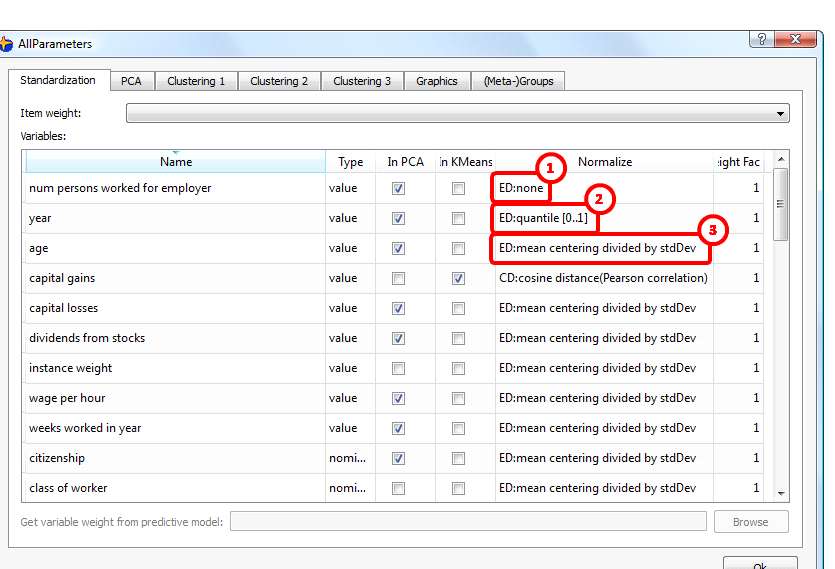
oNon-normalized original axis 
of the data: select “ED:none” inside the “Normalize” column inside the large table on the “Standardization” tab inside the 
parameter window (this tab is NOT accessible with the 
button, only with the button. See illustration: 
oNormalized-axis. There are two type of normalization:
▪Standard Normalization for inclusion inside an Euclidean-Distance:
... where 
is the ith column of the dataset that has been normalized
is the ith column of the dataset
is the mean of the ith column of the dataset
is the standard devidation of the ith column of the dataset
Select “ED: mean centering divided by StdDev” in the same table: 
▪Quantile Normalisation: 
Select “ED:quantile [0..1]” in the same table: 
q(x) is an operator that gives as output a number between 0 and 1.
The q(x) operator on a column C of the database is computed this way:
•Sort in increasing order all the numbers in C and remove all the duplicates. We obtain a new “sorted” column 
.
•
Thus, q(x) is zero when x is the smallest number inside the column C
and q(x) is one when x is the largest number inside the column C.
The Euclidean-distance between two rows of the dataset (between the two points A and B) is 
and is defined this way:
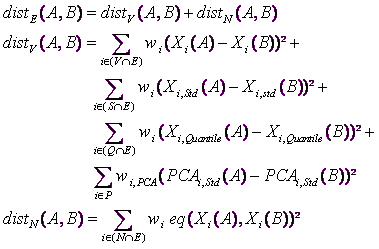
... where 
is a distance based on variables that only contains continuous numbers (values)
is a distance based on nominal variables only.
E is the set of “active” variables to include inside the Euclidean distance-definition.
V is the set of non-normalized continuous variables
S is the set of continuous variables that have been normalized using the “Standard” normalization
Q is the set of continuous variables that have been normalized using the “Quantile” normalization
N is the set of Nominal variables
P is the set of “active” PCA axises
eq(x,y) is an operator that returns one if the string ‘x’ equals ‘y’ and zero otherwise.
is the content of the column ‘i’ and row ‘A’ of the dataset
and 
have been defined on the previous page.
is the 
axis after a “Standard” normalization
and 
are user-specified (column-)weights.
The default values are: the sets V,S,Q,E are empty, the set S contains all the continuous variables, the set P contains the first ten PCA axises, the weights 
and 
are all one.
If some variables are included inside a “cosine-distance” (the C set is non-empty), then the distance-definition between two points A and B is:
...where
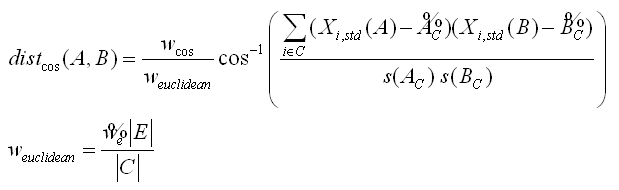
... and where C is the set of variables that are, at the same time, included inside the “cosine-distance” (column “normalize”) and that are “active” (column “In K-Means”).
is the number of variables inside the set
is a user-defined parameter that specified the relative weight of the cosine-distance compared to the Euclidean-distance.
is the average of the 
and 
user-specified weights included inside the Euclidean-distance
is the mean of a vector composed by the value of the columns 
with 
on the row A
is the Standard deviation of a vector composed by the value of the columns 
with 
on the row A
The default values are: the set C is empty, the weight 
You can define the sets E,C here: You can define the sets V,S,Q,C here: You can define 
here:
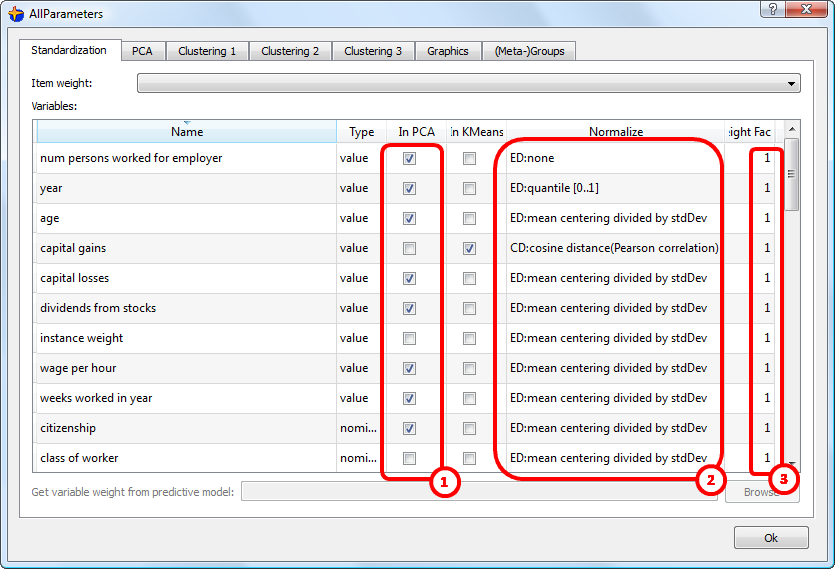
You can define the sets E,C,P here: You can define 
here:
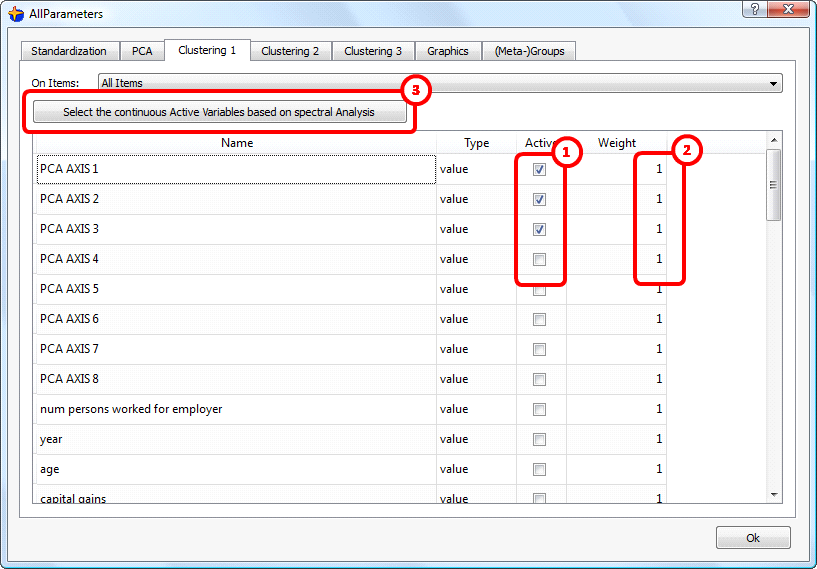
To help you to select the set P of the active PCA axises, you can click here:
When you click the 
button, the following window appears:
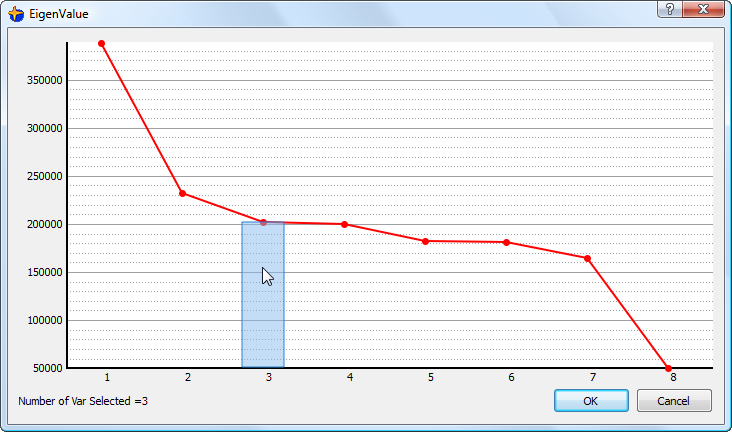
Please refer to the section 2.2.5 to know how to select to right number of PCA axises to include inside your “distance-definition”.
The default, initial setting for the “distance-definition” is equivalent to the following “distance-definition”:
